Faiss的基本使用

1. Faiss简介

Faiss（Facebook AI Similarity Search）是一个用于高效相似性搜索和密集向量聚类的库。它包含了能够在任意大小的向量集合中进行搜索的算法，甚至适用于那些可能无法完全装入内存的数据集。此外，Faiss 还包含了评估和参数调优的支持代码。Faiss 用 C++ 编写，并为 Python/numpy 提供了完整的接口。其中一些最有用的算法实现了 GPU 支持。

Faiss 提供了多种相似性搜索方法。它假设实例以向量形式表示，并通过整数进行标识，这些向量可以通过 L2（欧几里得）距离或点积进行比较。与查询向量具有最短 L2 距离或最大点积的向量被认为是相似的。Faiss 还支持余弦相似度，因为这是在归一化向量上的点积。

GPU 实现可接受来自 CPU 或 GPU 内存的输入。在配备 GPU 的服务器上，GPU 索引可作为 CPU 索引的直接替代品使用（例如，将 IndexFlatL2 替换为 GpuIndexFlatL2），并自动处理与 GPU 内存的复制。如果输入和输出都保留在 GPU 上，结果将更快。Faiss 支持单 GPU 和多 GPU 使用。

2. Faiss的安装

安装CPU版本：

pip install faiss-cpu

安装GPU版本（PyPI上的faiss-gpu版本较为落后，只有1.7.2）：

conda install -c pytorch faiss-gpu

建议安装1.7.4及以上的版本。其中faiss-gpu仅支持Linux系统。

3. IndexFlatL2/IndexFlatIP

3.1 Index概念

Faiss 的核心是 Index，即索引，这个概念可能听起来有些抽象。我们可以暂且认为它是一个「数据库」，我们可以通过它的 add 方法将若干个向量添加到这个数据库中，通过它的 search 方法来在数据库中检索与给定的查询向量最相似的前 k k k 个向量。

Index 中最常用的要属 IndexFlatL2 和 IndexFlatIP 了，本节也将重点讲解这两个。

顾名思义，IndexFlatL2 是根据L2距离来衡量向量之间的相似度，两个向量之间的L2距离定义如下：

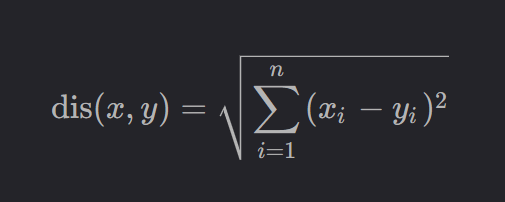
L2距离越短，说明两个向量之间越相似。但 IndexFlatL2 在实际计算的时候并不会开根号，因为执行开根号不仅会降低计算效率，还会降低数值稳定性。

IndexFlatIP 则是根据内积（Inner Product）来衡量向量之间的相似度，两个向量之间的内积定义如下：

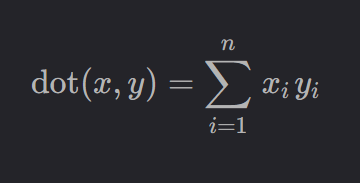
内积越大，说明两个向量之间越相似。

📝 Flat 的意思是，入库的向量不会经过任何形式的预处理（例如归一化）或量化，它们以原始的、完整的形式存储。并且在进行相似度检索时，会完整地扫库一次（俗称暴力搜索），所以它的计算结果一定是全局最优的。

Faiss 中常见的索引类型：

1. Flat Indexes（Flat 索引）

IndexFlatL2: 用于 L2 距离（欧几里得距离）的精确搜索。
IndexFlatIP: 用于内积（点积）的精确搜索。
IndexFlat1D: 继承自 IndexFlatL2，为一维向量（数轴上的点）专门做了优化。

2. IVF Indexes（Inverted File，倒排文件索引）

IndexIVFFlat: 基于倒排文件的索引，使用 Flat 索引作为量化器。
IndexIVFPQ: 结合了倒排文件和乘积量化（Product Quantization, PQ）。
IndexIVFSpectralHash: 使用谱哈希进行索引。
IndexIVFFastScan: 优化了扫描速度的 IVF 索引。

3. PQ Indexes（Product Quantization，乘积量化索引）

IndexPQ: 使用乘积量化的标准索引。
Index2Layer: 二层 PQ 索引，用于更大的数据库。

4. HNSW Indexes（Hierarchical Navigable Small World，分层导航小世界索引）

IndexHNSWFlat: HNSW 算法与 Flat 索引的结合。
IndexHNSWPQ: HNSW 算法与 PQ 索引的结合。
IndexHNSWSQ: HNSW 算法与标量量化（Scalar Quantization）的结合。

5. LSH Indexes（Locality-Sensitive Hashing，局部敏感哈希索引）

IndexLSH: 基于局部敏感哈希的索引。

3.2 IndexFlatL2的使用

这里以 IndexFlatL2 为例，因为 IndexFlatIP 的使用与它如出一辙。

根据源码描述

class Index(object):
    r"""
     Abstract structure for an index, supports adding vectors and searching them.

    All vectors provided at add or search time are 32-bit float arrays,
    although the internal representation may vary.
    """

可以得出

⚠️ 入库向量和查询向量都需要保证是 np.float32 型的。虽然numpy创建的浮点向量默认是 np.float64 型的，但经博主验证，不需要用 astype 转换也可以正常执行入库和检索操作。但如果是整型向量，则必须要转换。

示例：

import numpy as np
import faiss

np.random.seed(42)

num_vectors = 1000
dim = 64

# 创建1000个向量，每个向量的维度是64
vectors = np.random.rand(num_vectors, dim)
# 创建基于L2的索引
index = faiss.IndexFlatL2(dim)
# 将向量入库
index.add(vectors)

# 创建5个查询向量
queries = np.random.rand(5, dim)
# 要检索的近邻数量
k = 3
# D是距离数组，I是索引数组
D, I = index.search(queries, k)

print("查询结果:")
print("距离:\n", D)
print("索引:\n", I)

输出：

查询结果:
距离:
 [[6.099058  6.650052  6.803897 ]
 [6.2252884 6.445645  6.5882893]
 [6.649529  7.7154484 7.866695 ]
 [6.9578114 6.9743586 7.126388 ]
 [5.6874714 6.157484  6.350458 ]]
索引:
 [[502 606 234]
 [650 699 444]
 [432 629 451]
 [515  38 733]
 [303 919  33]]

距离数组 D 和索引数组 I 的形状均为 ( n , k ) (n,k) (n,k)，其中 n n n 是查询的数量， k k k 是要检索的近邻数量。其中 D[i, j] 代表数据库中距离第 i i i 个查询第 j j j 近的向量到该查询的距离，I[i, j] 代表数据库中距离第 i i i 个查询第 j j j 近的向量在数据库中的索引。

我们可以通过 I 来验证 D：

our_D = np.random.rand(5, 3)
for i in range(5):
    for j in range(3):
        dis_square = np.sum((queries[i] - vectors[I[i][j]]) ** 2)
        our_D[i][j] = dis_square

print(our_D)
# [[6.09905771 6.65005219 6.80389671]
#  [6.22528882 6.44564449 6.5882891 ]
#  [6.64952905 7.71544868 7.86669493]
#  [6.9578114  6.9743583  7.12638877]
#  [5.68747154 6.15748385 6.35045796]]

3.3 Index类的常用属性和方法

Index 类的一些常用属性：

print(index.d)  # 数据库中存储的向量的维度
print(index.ntotal)  # 数据库中有多少个向量
print(index.is_trained)  # 输出为True代表该类不需要训练或者已经训练结束
# Flat索引均不需要参与训练，向量入库后可直接进行检索
# 需要训练的类，则是需要先进行训练再进行向量入库

Index 类的一些常用方法：

class Index(object):

    def add(self, x):
        """ x 是将要入库的向量，x 的形状为 (num_samples, dim)，Index 会按照入库顺序为向量分配索引。"""
        pass

    def search(self, queries, k):
        """ queries 是待查询的向量，形状为 (num_queries, dim)，k 是要检索的近邻数量。"""
        pass

    def assign(self, queries, k):
        """ 与 search 的区别在于，assign 只返回 I 数组，而 search 会同时返回 D 数组和 I 数组。"""
        pass

    def train(self, x):
        """ 对于某些 Index 类，需要先根据向量进行训练，再添加向量。
            判断一个 Index 需不需要训练可以在它实例化之后立刻打印 index.is_trained，如果输出为 False 说明该类需要训练。
        """
        pass

    def reset(self):
        """ 清空库中的所有向量。"""
        pass

    @overload
    def reconstruct(self, i):
        """ 获取数据库中索引为 i 的向量。"""
        pass

    @overload
    def reconstruct(self, i, output_vec):
        """ 获取数据库中索引为 i 的向量并将该向量保存到 output_vec 中。"""
        pass

    def merge_from(self, otherIndex, offset=0):
        """ 将另一个索引合并过来。
            注意 offset 是偏移量，它会被加到 otherIndex 中所有向量的 ID 上，有助于保持唯一的标识符。
            通常 offset 可设置为 self.ntotal。
        """
        pass

注意，向量一旦入库后，就不可以被修改了，除非删除再重新添加。此外，Index 并不原生支持查看其中存储的向量，但是我们可以巧用 reconstruct 来查看：

np.random.seed(42)

vectors = np.random.randint(0, 9, (10, 16))

index = faiss.IndexFlatL2(16)
index.add(vectors)

content = np.empty_like(vectors).astype(np.float32)
for i in range(len(vectors)):
    index.reconstruct(i, content[i])
print(np.all(content == vectors))
# True

3.4 IndexIDMap

默认情况下，每个向量的索引是按照它们入库的顺序进行分配的。但有些时候，我们希望自己给这些向量分配ID，这时候就需要用上 IndexIDMap 了。

具体来讲，IndexIDMap 是一个包装器（wrapper），它在任何 FAISS 索引的基础上工作。首先创建一个基础索引（例如，IndexFlatL2 用于 L2 距离），然后使用 IndexIDMap 将这个索引包装起来。这样，基础索引负责计算向量间的相似性，而 IndexIDMap 负责处理与这些向量相关联的 ID。

注意，被包装的索引必须是空的，否则会报错：

np.random.seed(42)

num_vectors = 10
dim = 16

vectors = np.random.rand(num_vectors, dim)

index = faiss.IndexFlatL2(dim)
index = faiss.IndexIDMap(index)

然后我们使用 add_with_ids 来手动为要入库的向量分配索引，这里以倒序分配为例

ids = np.arange(num_vectors)[::-1]
index.add_with_ids(vectors, ids)

如果需要按照ID去删除向量的话，需要先创建一个selector，然后调用 remove_ids 方法（注意，IndexFlatL2 本身就支持该方法）：

np.random.seed(42)

num_vectors = 10
dim = 16

vectors = np.random.randint(0, 9, (num_vectors, dim))
print(vectors)

index = faiss.IndexFlatL2(dim)
index.add(vectors)

ids_to_remove = np.array([3, 5], dtype='int64')
id_selector = faiss.IDSelectorBatch(ids_to_remove)
index.remove_ids(id_selector)

removed_vectors = np.zeros((num_vectors - 2, dim)).astype(np.float32)
for i in range(len(removed_vectors)):
    index.reconstruct(i, removed_vectors[i])
print(removed_vectors)

执行该代码可以看到索引为3和索引为5的向量的确被移除了。

3.5 Index的存储/读取

保存：

faiss.write_index(index, "path_to_save_index/index_file")

读取：

index = faiss.read_index("path_to_save_index/index_file")

后缀名通常选用 .index。

Ref

[1] https://blog.csdn.net/weixin_43508499/article/details/119565802
[2] https://zhuanlan.zhihu.com/p/357414033
[3] https://github.com/facebookresearch/faiss?tab=readme-ov-file

目录CONTENT